Module 5
Reinforcement Learning
"Anhand des Beispiels eines Roboters, welcher in einem Labyrinth Batterien finden muss, werden neue Probleme aufgezeigt, mit welchen man zuerst noch gar nicht rechnet."

Über das Modul
Dieses Modul handelt von Reinforcement Learning (RL). Ziel ist es, den Schüler*innen ein grundlegendes Verständnis dafür zu vermitteln, was RL ist, wie es funktioniert und was häufige Probleme und Fallstricke sind. Der Fokus liegt eher auf praktischen Übungen, daher werden die Schüler*innen einerseits in die Rolle von selbstlernenden Algorithmen schlüpfen und erleben, wie der Trainingsprozess abläuft, und andererseits gegen lernende KIs spielen und diese trainieren.
Ziele
Schüler*innen sind in der Lage
- die Grundidee von RL zu erklären
- die Kern-RL-Schleife und Entscheidungen basierend auf Q-Werten zu verstehnen
- einschätzen zu können, eine Anwendung RL verwendete
- Probleme und Einschränkungen von RL zu benennen
Agenda
| Zeit | Inhalt | Material |
|---|---|---|
| 30 min | Einführung | Folien |
| 20 min | Übung - Münzspiel | Folien, Spielfeld, Aktionen |
| 20 min | Übung - Hexapawn | Online |
| 20 min | Übung - Menace | Online |
| 30 min | Übung - Labyrinth | Folien, Einfaches Labyrinth, Erweitertes Labyrinth |
| 15 min | Quiz - Richtig oder falsch? | Folien |
Einführung
In der Einführung geht es darum, dass sich die Schüler*innen mit grundlegenden Konzepten und Begriffen vertraut machen, die im Reinforcement Learning (RL) verwendet werden. Es basiert auf den Folien, die nicht nur gängige Anwendungen vorstellen, sondern die allgemeine Idee, wie eine KI durch das Ausführen und Auswerten von Aktionen selbstständig lernen kann.
Beispiele aus der Praxis
Die Folien starten mit der Einführung in das RL mit einem kurzen Video über eine selbstlernende Versteck und Such KI OpenAI. Wenn die Schüler*innen Englisch nicht gut genug verstehen, können entweder automatisch übersetzte Untertitel verwendet werden oder der Lehrer/die Lehrerin kann sich um das Übersetzen / Erklären kümmern.
Der wichtigste Punkt ist es verständlich zu machen, dass die KI in RL von selbst lernt, ohne direkte Anleitung der Programmiererin/des Programmierers. Den Agenten im Video wurde nie gesagt, wie man Dinge macht, nur was sie tun können und was ihr Ziel ist.
Nach dem Video ist das nächste Beispiel Leela Chess Zero (Lc0), eine moderne Schach KI, trainiert mit Reinforcement Learning. Während traditionelle Schach-KIs statische Funktionen verwenden, um Brettpositionen zu bewerten (wie das Erhalten von Fixpunkten für materielle Unterschiede und Figurenpositionen), lernte Lc0, was gute Positionen sind, indem sie Millionen von Partien gegen sich selbst und andere Spieler*innen spielte, und kann daher bessere Entscheidungen darüber treffen, welche Aktionen zu ergreifen sind. Es ist wichtig anzumerken, dass moderne Schachengines menschlichen Spieler*innen weit überlegen sind, selbst die besten Großmeisterspieler*innen können mit einem Smartphone geschlagen werden.
Der Grund, warum Spiele in der RL-Forschung sehr beliebt sind, ist, dass es gut definierte Regeln gibt, die es einfacher machen, konkrete Aktionen und Ziele zu definieren, die benötigt werden, damit RL funktioniert. Dies wird nach den Beispielfolien näher erläutert.
Da Schachengines immer noch meist Züge auf ähnliche Weise berechnen wie in den späten 90ern, als sie begannen, menschliche Spieler*innen konsequent zu schlagen3, werden sie manchmal aufgrund der "Einfachheit" des Spiels heruntergespielt. Dennoch haben sich RL-Algorithmen weiterentwickelt und können heutzutage in viel komplexeren Szenarien mit menschlichen Spieler*innen mithalten. Daher geht es im dritten Beispiel um AlphaStar, eine KI aus Googles Deepmind-Forschungsabteilung, die gelernt hat, ein komplexes modernes Computerspiel auf einem Niveau zu spielen, das mit den besten menschlichen Spieler*innen vergleichbar ist.4 Angesichts der Tatsache, dass es zu jedem Zeitpunkt ungefähr 1026 mögliche Aktionen gibt (im Vergleich zu Schach mit einem Durchschnitt von weniger als 40), ist es erstaunlich, dass die KI die besten Aktionen finden kann, obwohl sie sich zusätzliche Einschränkungen hält, die sie mit menschlichen Spielern und Spielerinnen vergleichbarer macht (eingeschränktes Sehvermögen, Reaktionszeit).
Das letzte Beispiel ist ein praktischeres zum Thema benutzerdefinierte Werbung (Ad). Es zeigt, dass RL auf viele verschiedene Arten verwendet werden kann, in diesem Fall als Umsatzoptimierung, indem gelernt wird, welche Anzeigen am häufigsten angeklickt (oder mit der Maus darüber bewegt) werden. Dadurch können zukünftige Anzeigen so angepasst werden, dass die Wahrscheinlichkeit, dass der Benutzer auf eine Anzeige klickt, maximiert wird.
Es gibt viele weitere Beispiele für Anwendungsfälle für RL, wie das Training selbstfahrender Autos mithilfe von Simulationen, aber diese Beispiele sind ein guter Ausgangspunkt, um sich nun mit der Frage zu befassen, wie ein Algorithmus tatsächlich von selbst lernen kann.
RL Basics
Um die Grundlagen von RL verstehen zu können, muss man zumindest einige Definitionen kennen, die in den ersten Folien vorgestellt wurden. Im Folgenden wird das Spiel TicTacToe als anschauliches Beispiel verwendet.
- Agent
- Ein Agent beschreibt die intelligente Entität, die mit der Umgebung interagiert und sinnvolle Entscheidungen treffen muss. Dies ist der Teil eines Programms, der die gesamte Logik und das Wissen der KI umfasst.
In TicTacToe wäre der Agent ein KI Spieler/ eine KI Spielerin. - Umwelt
- Damit ein Agent lernen kann, braucht er eine klar definierte Umgebung. Normalerweise ist die Umgebung eine Art Simulation einer realen Umgebung (wie eine simulierte Straße für ein Auto, um das Fahren zu lernen) oder ein Spiel.
In TicTacToe ist die Umgebung das Spielbrett mit den Markierungen (X,O) darauf. - Aktion
- Zu jedem Zeitpunkt muss der Agent entscheiden, welche Aktion zu ergreifen ist. Die verfügbaren Aktionen müssen jederzeit bekannt sein, die KI muss dann lernen, die beste Aktion auszuwählen.
In TicTacToe entspricht das Zeichnen des eigenen Symbols (X,O) auf ein freies Feld je einer möglichen Aktion. - Zustand (State)
- Ein Zustand (bzw. State) ist eine numerische Darstellung eines bestimmten Teils der Umgebung. Da Computer nur mit Zahlen arbeiten, können kritische Teile der Umgebung abstrahiert werden, um für die KI verständlich zu sein.
In TicTacToe könnte der Zustand eine Zahl für jede der neun Kacheln sein (z.B. 0 = leer, 1 = X, 2 = O) und vielleicht auch eine Zahl, wer an der Reihe ist (1 oder 2). In einem anderen Beispiel, dem Münzspiel, das in der folgenden Übung verwendet wird, ist der Zustand einfach die Anzahl der Münzen auf dem Tisch.
Diese Definition ist für viele sehr abstrakt, durch die folgenden Übungen wird es dann aber leichter verständlich. - Belohnung
- Die Belohnung ist im Allgemeinen ein numerischer Wert, der die Qualität oder das Ergebnis eines Zustandes darstellt. Normalerweise ist sie positiv im Falle eines guten Ergebnisses und negativ im Falle eines schlechten Ergebnisses.
In TicTacToe könnte die Belohnung +1 für einen Sieg, -1 für eine Niederlage und 0 für ein Unentschieden.
Schließlich müssen die Schüler*innen darüber nachdenken, was Agenten, Zustände, Aktionen und Belohnungen in den folgenden Beispielen sind. Dies kann auf vielfältige Weise angegangen werden, von einer einfachen Gruppendiskussion bis hin zu Präsentationen in kleinen Gruppen, die Methodenseite beinhaltet weitere Ideen.
- Leela Chess Zero
- Der Agent ist die Schach KI, der Zustand besteht aus numerischen Werten, die die Figuren auf dem Brett darstellen. Aktionen sind die möglichen Schachzüge und die Belohnung kann eine sehr hohe/niedrige Zahl für Gewinnen/Verlieren sein aber auch kleinere Zahlen dazwischen die angeben, wie "gut" die neu entstandene Position für die KI ist.
- OpenAI Verstecken und Suchen
- DieAgenten sind die Verstecker und die Sucher. Der Zustand beinhaltet Zahlen für die Position der Agenten sowie aller Objekte und zusätzlich Informationen ob sie gesperrt sind oder nicht (und von wem). Aktionen umfassen das Bewegen in verschiedene Richtungen, das Drehen und Greifen sowie das Versperren von Objekten. Die Belohnung kann die Anzahl der Sekunden sein, in denen die Verstecker nicht gefunden wurden, was auch als negative Zahl für die Sucher verwendet werden kann.
- Benutzerdefinierte Werbung
- Die Agenten können einzelne Werbespots sein, der Zustand könnte Informationen über die Art der Werbung beinhalten, sowie ob der Benutzer darauf geklickt hat oder nicht. Aktionen können den Wechsel zu bestimmten Themen oder zu Werbung oder Arten von Werbung umfassen. Die Belohnung könnte eine Zahl sein, die angibt, ob der Benutzer auf Hinzufügen geklickt hat oder nicht.
Q-Lernen
Die letzten Folien stellen das Konzept des Q-Lernen sowie die RL-Schleife vor. Es basiert auf dem Konzept von Aktion und Reaktion, bei dem der Agent mit der Umgebung interagiert, indem er eine auszuführende Aktion auswählt. Diese Aktion verändert die Umgebung und als Ergebnis erhält der Agent die Darstellung des neuen Zustandes sowie eine Belohnung, die angibt, wie gut die Aktion war. Angesichts dieser neuen Informationen kann der Agent dann sein Verhalten anpassen und dann eine neue auszuführende Aktion auswählen. Dieser Zyklus setzt sich fort, bis ein Ziel erreicht ist.
Q-Lernen basiert auf der RL-Schleife und speichert einen Qualitätswert (Q-Wert) für jedes Zustand- und Aktionspaar. Dieser Wert gibt an, wie "gut" die Aktion im aktuellen Zustand ist. Daher kann immer dann, wenn ein Zustand erreicht wird, die Aktion mit dem höchsten Q-Wert für ein optimales Verhalten ausgewählt werden. Da der Q-Wert am Anfang möglicherweise nicht korrekt ist (tatsächlich wird er häufig für jede Aktion zu Beginn auf einen Zufallswert gesetzt), kann er angepasst werden, indem er durch die Belohnung, welche für die Durchführung der Aktion erhalten wird, erhöht / verringert wird. Wenn dieser Vorgang oft genug wiederholt wird, erreichen die Q-Werte einen Punkt, an dem immer die "beste" Aktion ausgeführt wird.
Solange es nicht zu viele Zustand-Aktion-Paare gibt, können diese Werte in einer Tabelle gespeichert werden, in der jede Zeile aus einem Zustand und den Q-Werten aller verfügbaren Aktionen besteht.
Die Tabelle auf Folie 29 zeigt einen kleinen Ausschnitt aus einer solchen Q-Table für ein beispielhaftes Jump-n-Run-Spiel. Das Erreichen eines Diamanten wird mit +1 und das Fallen ins Wasser mit -1 belohnt. Die nächste Tabelle auf Folie 30 zeigt die gleiche Situation, aber mit einer fortgeschritteneren Tabelle, die zukünftige Belohnungen in ihre Aktion mit einbezieht. Dies bedeutet, dass eine Aktion, die dazu führen kann, dass Sie eine Aktion später ins Wasser fallen, auch eine kleine Strafe erhält.
Dieser Prozess der Anpassung der Q-Werte wird als Training bezeichnet. Während es manchmal möglich ist, eine KI während des normalen Gebrauchs zu trainieren, ist der Trainingsprozess oft unabhängig von der endgültigen Verwendung, da es Millionen von Iterationen dauern kann, um sinnvolle Werte zu erstellen.
Nach all dieser Theorie ist es an der Zeit, das Wissen an realen Beispielen zu testen, was zu den nächsten drei Übungen führt, die aufeinander aufbauen.
Material
Referenzen
Münzspiel
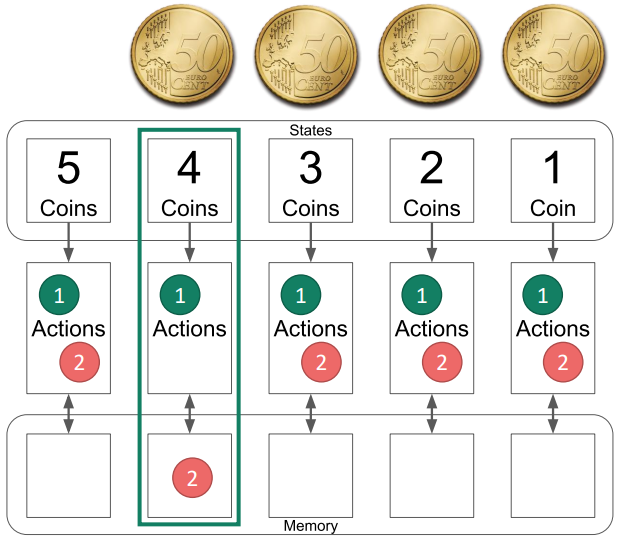
Diese Übung bietet eine Einführung in das RL-Lernen mit dem Münzspiel. Um das Grundkonzept zu verstehen, können die Folien als Einführung verwendet werden. Das Spiel erfordert eine Art von Token wie Münzen, Hütchen, Leckereien, ... in einer großen Menge, so dass jedes Schüler*innenpaar Zugang zu mindestens 5 von ihnen hat. Das Spiel beginnt damit, dass 5 Münzen auf einem Tisch liegen und die Spieler abwechselnd ein oder zwei davon wegnehmen. Der Spieler, der den letzten Spielstein nimmt, verliert.
Vorstellung des Spiels
Das Spiel wird mit den Folien 1-8 vorgestellt und die Schüler*innen können ein paar Spiele zu zweit spielen.
Einführung der KI
Einführung in die KI mit den Folien 9-35. Es wird empfohlen bereits vorher das Material (board and actions) zur Verfügung zu stellen, damit die Schüler*innen live sehen können, wie alles in der Realität aussieht und auch aktiv mit den Beispielen mitmachen können.
Lassen wir sie spielen
Dann dürfen die Schüler*innenpaare spielen, wobei eine*r die Rolle der KI übernimmt und der oder die andere normal spielt. Während die Spiele weitergehen, werden immer mehr Aktionen aus der KI entfernt, bis nur mehr die besten Aktionen übrig sind.
Die wichtigsten Erkenntnisse
Abschließend wird kurz über die wichtigsten Erkenntnisse diskutiert:
- Was passiert, wenn einige Zustände nie erreicht werden (z.B. wählt der Spieler/die Spielerin immer die gleichen Aktionen)?
- Nur aus Zuständen, die erreicht werden, wird gelernt. Wenn die KI während des Trainings nicht auf eine Situation stößt, findet sie möglicherweise nicht die richtige Bewegung.
- Wo lernt die KI in diesem Beispiel mehr, indem sie gewinnt oder verliert?
- Die KI in diesem Beispiel wird nur für das Verlieren bestraft, niemals für das Gewinnen belohnt, daher hat das Gewinnen keines Lerneffekt.
- Könntest du das Spiel so ändern, dass ein Sieg auch eine Art Belohnung bietet?
- Ja, zum Beispiel durch das Hinzufügen neuer Aktionssteine, wenn die KI gewinnt. Dann wird die KI eher eine der erfolgreicheren Aktionen auswählen. Dies wird in der nächsten Übung demonstriert.
Material
Hexapawn

Diese Übung baut auf dem Wissen der vorherigen auf (coin game) und basiert auf der Website https://www.stefanseegerer.de/schlag-das-krokodil/ und dem Spiel Hexapawn. In Hexapawn spielen zwei Spieler*innen auf einem 3 x 3 Brett gegeneinander. Dabei werden nur Bauern (von Schach) verwendet, die entweder ein freies Feld geradeaus bewegen oder einen gegnerischen Bauern diagonal schlagen können. Ein Spieler gewinnt, indem er entweder die Gegenseite mit einem Bauern erreicht oder den Gegner daran hindert, einen weiteren Zug zu machen (alle Bauern blockieren).
Demonstrieren der Website
Demonstrieren Sie zunächst die Funktionsweise der Website und erklären Sie die Spielregeln. Insbesondere die Einstellungen Reaktionszeit und nur mögliche Züge sollten erklärt werden, da sie bei den folgenden Aufgaben helfen. Darüber hinaus ist es wichtig, dass die Schüler*innen die Bedeutung der farbigen Punkte verstehen (entsprechen der gleichfarbigen Aktion) und sehen, dass diese Punkte entfernt oder hinzugefügt werden können.
Lassen wir sie spielen
Es ist an der Zeit, die Schüler*innen alleine spielen zu lassen. Ziel ist es, so oft wie möglich zu gewinnen, bevor die KI nicht geschlagen werden kann. Dies scheint eine einfache Aufgabe zu sein, aber bald werden die Schüler*innen erkennen, dass sie ein gutes Verständnis des Innenlebens benötigen, um über 10 oder sogar über 20 Siege zu erzielen. Achtung, wenn die Seite neu geladen wird, werden auch die Gewinne zurückgesetzt!
Die wichtigsten Erkenntnisse
Die wichtigsten Erkenntnisse ähneln denen des Münzspiel, sind jedoch ausgeprägter, da die Schüler*innen gezielt Züge machen müssen, die sie zuvor noch nicht verwendet haben, um die KI in unbekanntes Gebiet zu zwingen. Es ist auch gut ersichtlich, dass die Anzahl der möglichen Zustände mit der Anzahl der verfügbaren Aktionen recht schnell zunimmt. man kann sich leicht vorstellen, dass es auf einem größeren Brett (wie z.B. einem Schachbrett) so viele mögliche Zustände gibt (ungefähr 1044)1, dass es nicht möglich ist, eine KI von Hand zu trainieren oder sogar generell alle möglichen Zustände einzubeziehen.
Material
References
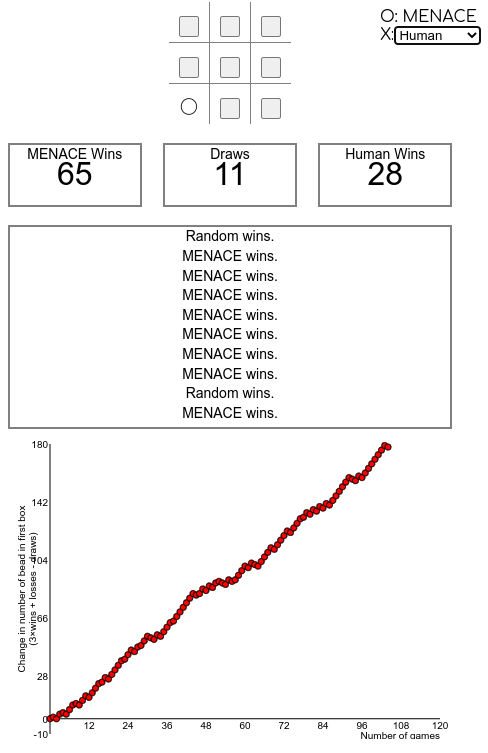
MENACE
Diese Übung baut wieder auf der vorherigen auf (Hexapawn) und führt ein Spiel mit noch mehr Zuständen ein, TicTacToe. Als gute Einführung kann der erste Teil dieses Videos von Matt Parker über MENACE verwendet werden. Es erklärt die Grundidee von MENACE, die dem Hexapawn-Beispiel von früher ähnelt, aber anstatt digital zu arbeiten, werden farbige Perlen in physischen Streichholzschachteln gelegt.
Während es eine interessante Idee sein könnte, ein solches System selbst mit der Klasse zu bauen, wird es wahrscheinlich viel Zeit in Anspruch nehmen (nicht nur um das ganze zu erstellen, sondern auch um es zu trainieren). Daher wird in dieser Übung ein Online-Simulator des Systems verwendet.
Einführung MENACE
Stellen Sie zunächst das MENACE-System, eine RL TicTacToe-Maschine, vor, indem Sie entweder das erste ~2:20min (oder mehr) dieses Videos von Matt Parker verwenden oder indem Sie diskutieren (oder in Gruppenarbeiten), wie das vorherige Beispiel so modifiziert werden könnte, dass es für das Spiel von TicTacToe funktioniert.
Demonstration der Website
Demonstrieren Sie dann, wie Sie den Simulator auf der Website verwenden https://www.mscroggs.co.uk/menace/, erklären Sie insbesondere die Bedeutung der Zahlen und Systeme rechts (Zustände und Q-Wert von Aktionen, höher = eher gewählt, gespiegelte Zustände sind ausgeschlossen) und wie Sie selbst Spiele spielen oder die KI gegen andere KIs spielen lassen können (wie die zufällig spielende KI oder eine perfekt spielende KI).
Lassen Sie sie ihre eigene KI trainieren
Angesichts des Wissens über die Nutzung der Website müssen die Schüler nun ihre eigene KI trainieren, die schlussendlich so gut wie möglich spielen sollte.
Sprechen Sie über die Probleme
Bald werden die Schüler erkennen, dass, auch wenn dies nach einer einfachen Übung klingt, wahrscheinlich keiner der Ansätze zu einer perfekt spielenden KI führen wird. Die Hauptgründe dafür sind:
- Die KI begegnet einigen Zustandes während des Trainings einfach nicht, so dass sie nicht weiß, was ein guter Zug ist, wenn sie ihnen begegnet. Dies geschieht zum Beispiel, wenn sie nur gegen eine perfekt spielende KI trainiert wird, wo sie nie lernt, dass sie tatsächlich auch gewinnen kann. Die KI lernt also nie Fehler des Gegenspielers auszunützen.
- Die KI lernt falsche Züge, weil der Gegner nicht richtig reagiert hat. Zum Beispiel könnte Sie gelernt haben, dass ein Zug normalerweise zum Sieg führt, weil der Gegner nur schlechte (oder zufällige) Züge macht, aber wenn der Gegner richtig spielt, wird die KI verlieren.
Das technische Problem dahinter ist Exploration vs. Exploitation1, das in der nächsten Übung näher untersucht wird.
Material
Referenzen
Maze
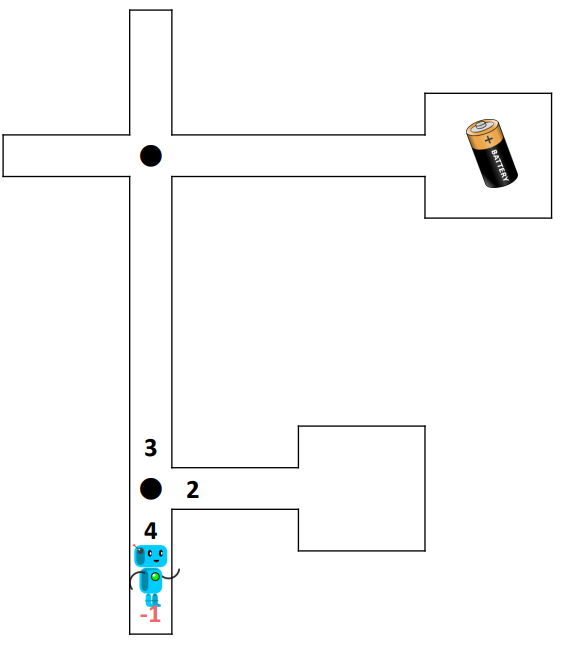 Anhand des Beispiels eines Roboters, welcher in einem Labyrinth Batterien finden muss, werden neue Probleme aufgezeigt, mit welchen man zuerst noch gar nicht rechnet. Die Übung beginnt mit diesen Folien und erklärt das Szenario eines Roboters in einem Labyrinth, der eine Batterie finden muss. Am Anfang nimmt der Roboter zufällige Wege und lernt im Laufe der Zeit den richtigen Weg zu seinem Ziel. In der zweiten Übung beinhaltet das Labyrinth mehrere Batterien mit unterschiedlichen Belohnungen, was zu suboptimalen Ergebnissen führen kann, wie im letzten Teil der Folien erklärt.
Anhand des Beispiels eines Roboters, welcher in einem Labyrinth Batterien finden muss, werden neue Probleme aufgezeigt, mit welchen man zuerst noch gar nicht rechnet. Die Übung beginnt mit diesen Folien und erklärt das Szenario eines Roboters in einem Labyrinth, der eine Batterie finden muss. Am Anfang nimmt der Roboter zufällige Wege und lernt im Laufe der Zeit den richtigen Weg zu seinem Ziel. In der zweiten Übung beinhaltet das Labyrinth mehrere Batterien mit unterschiedlichen Belohnungen, was zu suboptimalen Ergebnissen führen kann, wie im letzten Teil der Folien erklärt. Vorstellung des Spiels
Führen Sie die Schüler zunächst mit den Folien 1-18 in das Spiel ein. Stellen Sie dann jedem Schüler (oder Schülerpaar) eine Kopie des RL Maze Basic, einen Würfel und einen Stift zur Verfügung.
Lassen wir sie spiele
Dann müssen die Schüler*innen mehrere Runden spielen, bis der Weg zur Batterie klar definiert ist. Um Werte zu aktualisieren, kann man sie einfach durchstreichen und den neuen Wert daneben schreiben. Einige Schüler*innen werden "Glück" haben und der Weg wird sich sehr schnell bilden, bei anderen wird der Roboter in jede Sackgasse laufen, bevor er sein Ziel erreicht. Wenn einige Schüler*innen viel zu schnell sind, können sie es erneut mit einem neuen Blatt desselben Labyrinths versuchen und beobachten, ob es sich beim zweiten Mal anders verhält.
Stellen Sie das erweiterte Labyrinth vor
Stellen Sie jedem Schüler, jeder Schülerin (oder Schülerpaar) eine Kopie der RL Maze Advanced zur Verfügung und lassen Sie sie erneut ihren Roboter trainieren. Auch wenn diesmal mehrere Batterien vorhanden sind, kehrt der Roboter immer sofort zum Anfang zurück, wenn er eine Batterie erreicht. Das Spiel ist wieder vorbei, wenn der Roboter einen festen Weg zu einer der Batterien hat, auch wenn es nicht unbedingt diejenige mit dem höchsten Belohnung ist.
Finden Sie das Problem heraus und schlagen Sie Lösungen vor
Wenn alle fertig sind, haben verschiedene Roboter unterschiedliche Punktzahlen erreicht. Erstellen Sie nun Gruppen von etwa 4 Schüler*innen und lassen Sie sie diskutieren, warum einige Roboter besser abgeschnitten haben als andere, sowie auch eine mögliche Lösung ausarbeiten. Es könnte hilfreich sein, Schüler*innen mit unterschiedlichen Punktezahlen zusammenzufassen, damit sie das Problem besser visualisieren können. Dann muss jede Gruppe ihre Erkenntnisse und Lösungen präsentieren.
Erklärung des Problems
Verwenden Sie schließlich Folien 19-26, um den Kompromiss zwischen Exploration und Exploitation1 sowie mögliche Lösungen für diese Übung zu diskutieren.
Optional: Testen verschiedener Lösungen
Stellen Sie neue Kopien des RL Maze Advanced bereit, damit die Gruppen verschiedene neue Ansätze (z. B. unterschiedliche Explorationsraten) testen können.
Material
References
Richtig oder falsch?
Dieses letzte Kapitel dient als Zusammenfassung des gesamten Moduls. Es basiert auf einem Quiz mit zehn richtig oder falsch Fragen und regt die Schüler*innen an, über alle Aspekte nachzudenken, die sie gelernt haben.
Das Quiz selbst besteht aus Folien, die eine Frage nach der anderen anzeigen, bevor die richtigen Antworten angezeigt werden. Daher können die Schüler*innen ihre Antworten aufschreiben und am Ende ihre Punktzahl berechnen. Es wird dringend empfohlen, nach der Enthüllung der Antwort auf jede Frage eine Pause einzulegen, um kurz zu diskutieren, warum sie richtig oder falsch ist. Alternativ kann diese Übung auch in Gruppen durchgeführt werden, um die Diskussion zwischen den Schülern*innen weiter zu fördern.